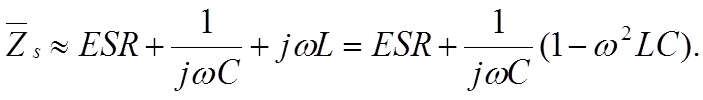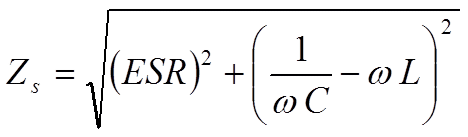C1.3 LOSSES
C 1.3.1 Impedance and ESR
A capacitor creates in AC circuits a resistance, the capacitive reactance (Formula C1-3). There is also certain inductance in the capacitor. In AC circuits it produces an inductive reactance that tries to neutralize the capacitive one. Finally the capacitor has resistive losses. Together these three elements produce the impedance, Z.
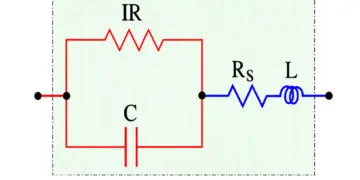
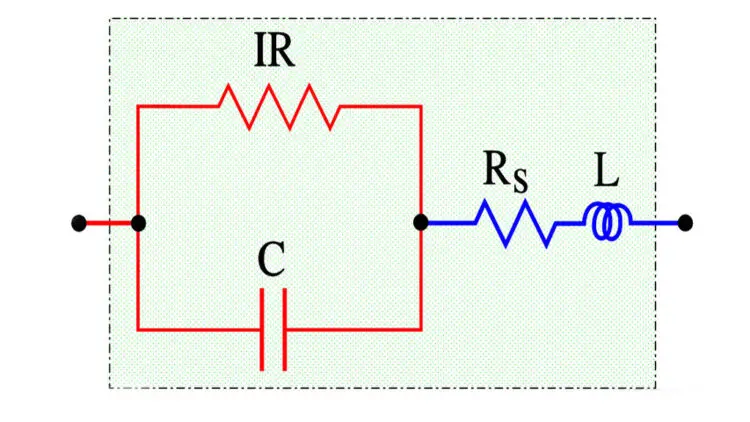
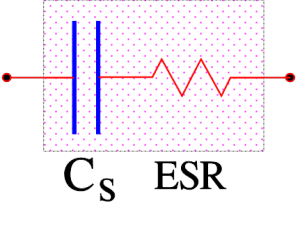
If we apply an AC voltage over a capacitor its losses release heat. They can be regarded as a resistive part of the impedance, i.e., as resistive elements distributed in different parts of the component, e.g. in accordance with the equivalent circuit in Figure C1-16.

- C = Capacitance
- IR = Insulation Resistance (IR>>Rs)
- Rs = Series losses
- L = Inductance in lead-in wires
Rs consists of resistance in lead-in wires, contact surfaces and metallized electrodes, where such elements occur, as well as dielectric losses. If we apply a DC voltage over the capacitor, the generator ”feels” a purely resistive loss dominated by the IR. But because of the high value of the IR the heat release will be negligible. Should we instead change over to an AC voltage and let the frequency rise the current will increase proportionally and eventually release a considerable heat in the Rs. If we transform the IR to a small series resistance with the help of formula C1-14 and join it with the Rs we get a total series resistance called ESR (Equivalent Series Resistance, sometimes called Effective Series Resistance). The series impedance, Zs, in Figure C1-16 can be written:
As a root mean square value we obtain the formula:
The capacitive reactance, 1/ωC, in the formula above decreases with frequency to that level where the inductive reactance, L, takes over. It happens at the resonance frequency fo of the capacitor where 1/ωC = L. Above the resonance frequency the capacitor is inductive. Exactly at the resonance frequency remains of the impedance Z only the resistive ESR (Figure C1-17). By determining the losses at the resonance frequency we gain accuracy. But there is a condition for this accuracy. We need to know the frequency dependence of the ESR which very much is conditioned by the dielectric material. In certain materials it is negligible, in others considerable. Some guidance is obtainable through those frequency diagrams which sometimes are shown in this book for certain dielectric materials where this information is of importance.
The expression for capacitance in the formula for Zs above can be simplified to a series capacitance Cs. If C means the nominal capacitance then we obtain Cs as
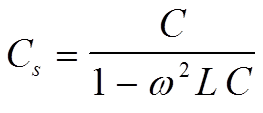
………………………… [C1-10]
and
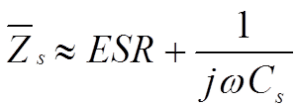
………………………… [C1-11]
The equivalent circuit diagram then looks like the one in Figure C1-18.
Impedance around the resonance frequency
Figure C1-17 shows an example of the impedance diagram around the resonance frequency. We shall evolve the reasoning further.
Because of the approximations used during derivation of formula C1-10 it applies only far below the resonance frequency, f0. There, however it may cause discernible deviations from the true value. Already at 0.2 x f0 Cs will be approximately 4% greater than the nominal value C.
Often the expression for Cs is used when the frequency dependence of capacitance is shown in diagrams. This means that the capacitance quite contrary to physical and electrical laws starts rising at higher frequencies. The explanation accordingly is to be sought in errors in the measurement method.
Except for electrolytics and other high loss capacitors the impedance curve usually has the appearance of the one shown in Figure C1-19.
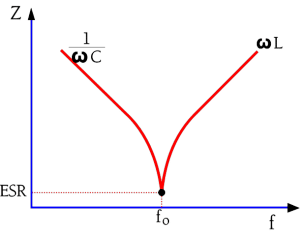
The sharp tip at the resonance frequency is typical for capacitors with comparatively small losses. In this frequency range the impedance contribution from the ESR is smaller than those of the capacitive and inductive reactances. When the decreasing capacitive reactance reaches the same magnitudes as those of the rising inductive reactance there will be an increasing influence from the latter. It reduces the capacitive reactance and eventually eliminates it. The curve bends down in a sharp tip. The bottom of the bend is determined by the ESR.
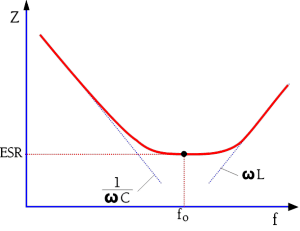
In capacitors with relatively high losses, for example electrolytics, the impedance curves reach and are influenced by these losses long before we get to the resonance frequency. A frequency dependent decrease in capacitance may also play a certain role in the frequency range. The impedance curve will deviate from the initial reactance curve and level out in a pliable bend on the ESR contribution, high above the point of intersection between the capacitive and inductive branch. The phenomenon is illustrated in Figure C1-20.
C 1.3.2 Loss Dependent Derating
The heat release from AC applications limits the temperature range of for example paper capacitors where the loss raises the internal temperature appreciably. While DC applications for example allow +85 or +100°C, AC applications already at 50 Hz may require limitations to maximum +70°C.
Higher frequencies require further derating because of the current which grows correspondingly. The R.M.S. value of the AC voltage furthermore is derated according to the permitted DC value not only with respect to the peak value and the temperature rise but also because of the additional strain that every repolarization exerts on the dielectric. The higher the rated voltage, the higher the degree of derating.
Example: AC/DC = 40/63, 63/100, 125/250, 220/400, 300/630, 500/1000, 660/1600. But please, always check what the relevant data sheets specify.
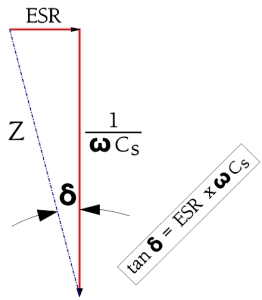
C 1.3.3 Dissipation Factor (DF) / Tanδ
The losses in Figure C3-18 are concentrated to the ESR which consequently becomes significant when we leave the low frequency range. For HF chips and high loss components as for example electrolytics often the ESR is stated in the data sheets. If the ESR information is missing you always find, for all component types, a specified dissipation factor (DF), the tanδ (Figure C1-21).
Hence at higher frequencies the series circuit according to Figure C1-18 applies. There is
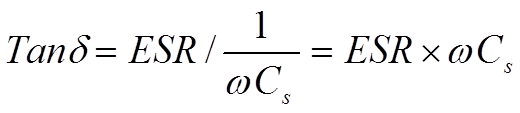
……………….. [C1-12]
Tanδ usually is expressed in %.
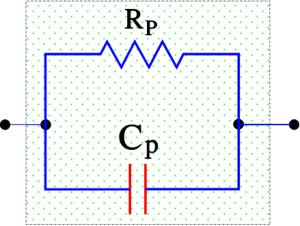
If the frequency declines to zero the circuit becomes resistive according to Figure C1-10 and -16, without any capacitance, and the losses are limited to the IR. Also at very low frequencies the IR is predominant but here it should be completed with dawning AC dependent losses to an equivalent loss resistance Rp. The diagram in Figure C1-16 now can be simplified to a parallel circuit with the capacitance Cp (Figure C1-22).
If we describe the impedance in a parallel circuit according to Figure C1-22 it’s easy to show that its dissipation factor – which applies at low frequencies – can be written as
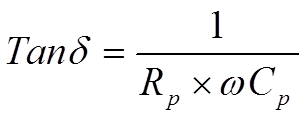
……………………………[C1-13]
The difference between Cs and Cp usually is negligible depending to the impedance value – see note below. We shall return to the connections in some formulas. If we equate the formula C1-10 with C1-11 we obtain
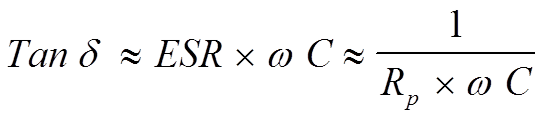
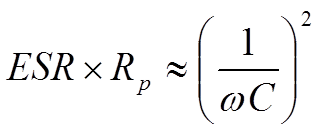
……………………………[C1-14]
Let us terminate the discussion about the capacitor losses by distinguishing the different types of losses as in following Figure C1-23.
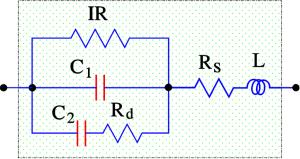
- Rd = dielectric losses
- Rs = losses in leading-in wires, joints and electrode metallizations
- ESR = Rs + Rd
- C = C1 + C2.
Cs,Rs or Cp,Rp ? What to use for impedance measure bridge set up ?
An impedance analyzer can measure the capacitance both in parallel or in series. The best fit circuit model will be depending on the value of capacitance of the capacitor.
When C is small and impedance is high, parallel impedance between C and Rp will become significantly higher than Rs. Thus the meter setting for measuring capacitance should be Cp. When C is large and impedance is small, parallel impedance for C and Rp is not as significant. Therefore, Cs should be used for the meter setting to measure capacitance.
A good rule of thumb to select the impedance setting is to use Cp for capacitor impedance values greater than 10kΩ and Cs for less than 10Ω.
ESR or DF ?
Another practical outcome is to think about what parameter is better for description of losses in capacitor – ESR or DF ? From the pure physics point of view, it does not matter, as together with a second parameter (capacitance or impedance), both parameter are describing the same stage of the capacitor. While ESR is an information about real losses only, DF combine information about real losses and reactive losses (but we need the second parameter anyway to describe the exact capacitor stage).
The same is true about ESR/DF frequency dependence. It does not matter if I use ESR or DF characterization for description at low or high frequencies from the basic physics. HOWEVER, the industry convention is to use DF for low frequency (120Hz or 1kHz) characterization, where dielectric losses are dominating and ESR for higher frequency (100kHz) behaviour, where resistive connection losses are the main part of the losses. You can find both DF and ESR values in manufacturer datasheets with reference to those frequencies.
Case study: you can hear people from industry saying: “that capacitor has a high DF” that means that the capacitor has a high losses in the lower frequency zone (120/1kHz) that could indicate some issue with dielectric material (impurities, delamination …). and of course, ESR at 120Hz/1kHz will be also high. The same is about ESR – when someone says: “ESR of the capacitor is a problem” he/she usually means reference to the standard measurement frequency 100kHz indicating problems with resistive losses (inter-connection issues, bad welds etc) … and of course DF at 100kHz would be also high.
C 1.3.4 Q value
Sometimes we encounter the expression Q or Q value, especially in high frequency applications. Instead of describing the capacitor losses as DF (Tanδ) we rather specify its freedom from losses, its figure of merit, the Q value. It is defined as
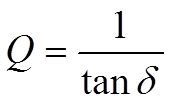
…………………….[C1-15]
Typical Q values for ceramic Class 1 dielectrics range from 200 to 2000 at 100 MHz and will vary strongly with frequency.
We shall use the Q value to describe the connection between the quantities in the series and parallel circuits in Figure C1-18 and -20. By depicting the expressions for the impedance and Q values of these circuits and equate the real and imaginary parts of the impedance we can show that
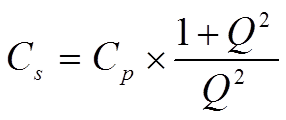
………………………………[C1-16]
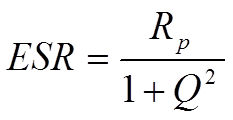
…………………………………….[C1-18]
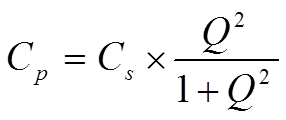
…………………………[C1-17]
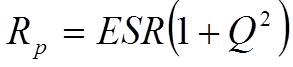
……………………………[C1-19]
C 1.3.5 Loss versus Frequency
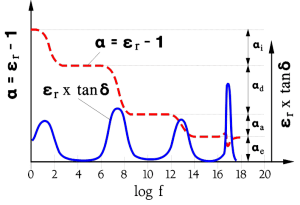
Figure C1-24 illustrates the behavior of different dielectric dipoles when they are affected by an alternating field. They will oscillate at the same frequency as the field’s if allowed by their reaction time. Every rotary motion requires energy and the executed work produces heat. The most inert dipoles will react to the very low frequencies and will here contribute to the losses. But as the frequency increases the different types of dipoles will not be able to respond quickly enough, one after another, as shown in the figure.
Just in the range where the reaction time of the dipoles and the frequency period coincide a kind of resonance occurs which causes the dipole types to react with a loss peak (Figure C1-24).
Observe that Figure C1-24 deals with dipole losses, nothing else. There are other dielectric materials which have no molecular dipoles. They are called non-polar while the others are called polar. This has nothing to do with the polarity dependence of electrolytics.
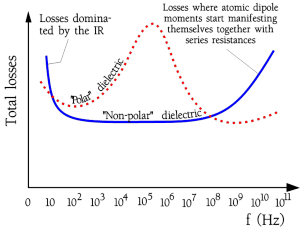
The sum of losses in a polar and a non-polar capacitor may look like the ones in Figure C1-25.
We shall remember that dielectric losses (material permittivity) may be frequency dependent and as per the basic capacitance calculation it is the only parameter responsible for capacitor frequency dependence in ideal capacitor (considering surface area of electrodes and thickness of dielectric stable). The real capacitor may have additional RLC ladder structure that limits its resonance and maximum operating frequency.
Capacitance (permitivity) and ESR frequency dependence can be also a good tool for failure analyses that may identify if there is additional (faulty) polarization caused by voids, impurities or which part of capacitor structure corresponding to higher losses etc.
ABC of CLR: Chapter C Capacitors
Capacitor Losses (ESR, IMP, DF, Q)
EPCI licenced content by:
[1] EPCI European Passive Components Institute experts original articles
[2] CLR Passive Components Handbook by P-O.Fagerholt*
*used under EPCI copyright from CTI Corporation, USA

This page content is licensed under a Creative Commons Attribution-Share Alike 4.0 International License.
see the previous page: Insulation Resistance
< Page 3 >
see the next page: Energy Content and Electromagnetic Force